Multivariate probit

In statistics and econometrics, the multivariate probit model is a generalization of the probit model used to estimate several correlated binary outcomes jointly. For example, if it is believed that the decisions of sending at least one child to public school and that of voting in favor of a school budget are correlated (both decisions are binary), then the multivariate probit model would be appropriate.

Example: bivariate probit

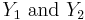$Y_1 \text{ and } Y_2$ are two binary dependent variables.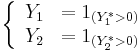 $\left\{ \begin{array}{ll} Y_1&=1_{(Y^*_1>0)}\\ Y_2&=1_{(Y^*_2>0)} \end{array} \right.$

with

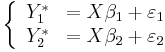
$\left\{ \begin{array}{ll} Y_1^*&=X\beta_1%2B\varepsilon_1\\ Y_2^*&=X\beta_2%2B\varepsilon_2 \end{array} \right.$

And:

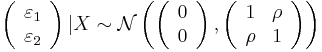
$\left( \begin{array}{c} \varepsilon_1\\ \varepsilon_2 \end{array} \right)|X \sim \mathcal{N} \left(\left( \begin{array}{c} 0\\ 0 \end{array} \right) , \left( \begin{array}{cc} 1&\rho\\ \rho&1 \end{array} \right)\right)$

Fitting the bivariate probit model involves estimating the values of 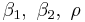$\beta_1,\ \beta_2,\ \rho$ .